Adversarial Lipschitz Regularization

By Dávid Terjék†

†Robert Bosch Kft.

Presented By

Andreas Munk

Nov 20, 2020

Penalization of Lipschitz constraint violation terjek2020adversarial

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Generative adversarial networks (GANS) goodfellow2014generative

  • A generator is a neural network \(g:\mZ\rightarrow\mX\subseteq\real^{D_{x}}\) which maps from a random vector \(\vz\in\mZ\) to an output \(\vx \in \mX\)
    • \(g\) characterizes a distribution \(p_{\theta}(\vx)\), where \(\theta\in\Theta\subseteq\mathbb{R}^{D_g}\) denotes the generator’s parameters
  • Aim is to match \(p_{\theta}\) with some real target distribution \(p_{\mr{real}}\)
  • A critic/discriminator \(f_\phi:\mX\rightarrow \mF\) with parameters \(\phi\in\Phi\subseteq\real^{D_f}\)

  • Generally we frame GANs as a minimax game,

    \[\min_{\theta}\max_{\phi}h(p_{\theta},f_\phi)\]

  • Originally Goodfellow et al. (2014) defined

\[ h(p_{\theta},f_\phi) = \E_{x\sim p_\mr{true}}\br{\log f_\phi(x)} + \E_{x\sim p_{\theta}}\br{\log (1 - f_\phi(x))}\]

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Wasserstein GAN arjovsky2017wasserstein

  • Wasserstein Distance \(W_{p}(P_{1},P_{2})=\paren{\inf_{\gamma\in\Gamma(P_{1},P_{2})}\E_{\gamma}\br{d(x_{1},x_{2})^{p}}}^{\frac{1}{p}}\)
  • Kantorovich-Rubinstein duality villani2008optimal, \[ W_{1}(P_{1},P_{2}) = \sup_{\norm{f}_{\mr{L}}\leq1}\paren{\E_{P_{1}}\br{f} - \E_{P_{2}}\br{f}} \]
  • WGAN: \[ \min_{\theta}\max_{\phi}\E_{p_\mr{true}}\br{f_{\phi}} - \E_{p_{\theta}}\br{f_\phi}, \quad \mr{s.t.}~\norm{f_{\phi}}_{\mr{L}}\leq 1\]
  • Notice the Lipschitz constraint \(\norm{f_{\phi}}_{\mr{Lip}}\leq 1\)
  • Constraint imposed using weight clipping \(\Phi\subseteq \mW = \br{-w,w}^{D_{f}}\), where \(w\) is some constant
    • Ensures global\(^{*}\) Lipschitz continuity with some unknown Lipschitz constant \(L\geq 0\)
      • \(^{*}\text{assuming}\) for all \(\phi\in\mW,~f_{\phi}\) is Lipschitz continuous or \(\mX\) is compact
      • Generally consider \(LW_{1}(P_{1},P_{2})\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Lipschitz Continuity

  • Definition: Given two metric spaces \(\paren{\mX, d_{\mX}}\) and \(\paren{\mY, d_{\mY}}\), a function \(f:\mX\rightarrow \mY\) is called Lipschitz continuous is there exists a constant \(L\geq 0\) such that

    \[\forall (x,x') \in\mX\times\mX, d_{\mY}(f(x),f(x')) \leq L d_{\mX}(x,x') \]

    In particular consider \(\mX\subseteq\real^{D_{x}}\) and \(\mY\subseteq\real^{D_{y}}\) and the Euclidean distance, then

    \[\forall (x,x') \in\mX\times\mX, \norm{f(x)-f(x')}_{2} \leq L \norm{x-x'}_{2}\]

  • For more information on Lipschitz continuity and deep neural networks, see e.g. virmaux2018lipschitz.
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Improved Wasserstein GAN (WGAN-GP) gulrajani2017improved

  • Weight clipping reduces the function space
  • Soft regularization by considering the Lipschitz constraint with respect to the optimal coupling \(\gamma^{*}\)
    • \(\gamma^{*}\) is unknown
    • Use interpolated samples \(\tilde{x}\sim p_{i}\) between \(x_{\mr{real}}\) and \(x_{\mr{fake}}\)
    • Sample \(x_{\mr{real}}\sim p_{\mr{real}}\), \(x_{\mr{fake}}\sim p_{\theta}\), and do a random interpolation
  • New objective using gradient penalties (GP) \[ \min_{\theta}\max_{\phi}\E_{p_\mr{true}}\br{f_{\phi}} - \E_{p_{\theta}}\br{f_\phi} + \lambda\E_{\tilde{x}\sim p_{i}}\br{\paren{\norm{\grad_{\tilde{x}}f_{\phi}(\tilde{x})}_{2} - 1}^{2}} \]
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Lipschitz Continuity and Differentiability

  • Using Theorem 3.1.6 in federer2014geometric, we have that if \(f:\real^{n}\rightarrow\real^{m}\) is locally Lipschitz continuous function, then \(f\) is differentiable almost everywhere (except for a set of Lebesque measure zero). If \(f\) is Lipschitz continuous, then

    \[L(f)=\sup_{x\in\real^{n}}\norm{D_{x}f}_{op},\]

    where \(\norm{\mX}_{op}=\sup_{\vv:\norm{\vv}=1}\norm{\mX\vv}_{2}\) is the operator norm of \(\mX\in\real^{n\times m}\)

  • In particular if \(m=1\), then \(D_{x}f = \trans{(\grad_{x}f)}\) and using Cauchy-Schwartz inequality we have,

    \[\norm{\trans{(\grad_{x}f)}}_{op}=\sup_{\vv:\norm{\vv}=1}\abs{\langle\grad_{x}f,\vv\rangle}\leq\sup_{\vv:\norm{\vv}=1}\norm{\grad_{x}f}\norm{\vv}=\norm{\grad_{x}f}\]

  • Choose \(\vv=\frac{\grad_{x}f}{\norm{\grad_{x}f}}\) such that

    \[L(f) = \sup_{x\in\real^{n}}\norm{\grad_{x}f}_{2}\]

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Can we do better?

  • Issues with WGAN-GP:
    1. \(p_{i}\) is generally not equal to \(\gamma^{*}\), even when \(p_{g}=p_{\mr{true}}\). \(p_{i}\) is constructed using random interpolations, and important correlations may be unaccounted for
    2. Too strong regularization. The gradient penalty term is fully minimized when \(\grad_{x}f(x) = 1\) for all \(x\)

  • petzka2018regularization addresses point (2), by instead using the regularizer \[\lambda\E_{p_{\tau}}\br{\max(0,\norm{\grad_{x}f(x)}_{2}-1)^{2}},\]

    where \(p_{\tau}\) is another random pertubation distribution similar to \(p_{i}\).

    • Only penalizes gradient norms bigger than one
    • \(p_{\tau}\) did not provide improvements compared to \(p_{i}\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Adversarial Lipschitz regularization (ALR) terjek2020adversarial

  • Previous methods impose soft Lipschitz constraints in the form of (estimated) expectations
    • Low probability of finding biggest violation of the Lipschitz constraint.

  • Consider the definition of Lipschitz continuity such that, \[\norm{f}_{L}=L=\sup_{x,x'\in\mX}\frac{d_{\mY}(f(x),f(x'))}{d_{\mX}(x,x')}=\sup_{x,x+r\in\mX}\frac{d_{\mY}(f(x),f(x+r))}{d_{\mX}(x,x+r)},\]

    where let \(x'=x+r\) and the supremum is with respect to both \(x\) and \(r\in\real^{n}\). To (approximately) ensure \(x+r\in\mX\), the Euclidean norm of \(r\) is bounded, \(\norm{r}_{2}\leq R\) for some \(R \gt 0\)

  • Assuming that for each \(x\in\mX\) the supremum is attained, we can substitute \(\sup\rightarrow\max\), and consider \[r'=\argmax_{x+r\in\mX}\frac{d_{\mY}(f(x),f(x+r))}{d_{\mX}(x,x+r)}\]
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

  • Under certain assumptions\(^{*}\) we can cast this problem into the following form

    \[r'=\argmax_{\norm{r}_{2}\leq R}d_{\mY}(f(x),f(x+r))\]

  • The Adversarial Lipschitz Penalty (ALP),

    \[ \mL_{\mr{ALP}} = \max\paren{0,\frac{d_{\mY}(f(x),f(x+r'))}{d_{\mX}(x,x+r')} - K}\]

    • Also considered the two-sided penalty (without \(\max(\cdot,\cdot)\)), but was found less stable.
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

\(^{*}\text{Assumptions}\)

  • Consider the optimization problem \[ r'=\argmax_{x+r\in\mX, \norm{r}_{2}\leq R}\frac{d_{\mY}(f(x),f(x+r))}{d_{\mX}(x,x+r)} \]
  • For an arbitrary inequality constraint, assume that:
    • \(r'\) must lie somewhere on the constraint boundary
    • \(d_{\mX}(x,x+r)\) is constant on the constraint boundary and takes on some value \(c\)
    • Assume further that \(d_{\mX}(x,x+r)\leq c\) for all \(r\) within the feasible region
  • If those assumptions are satisfied, we may ignore \(d_{\mX}(x,x+r)\)
  • In our case we have:
    • The constraint is written in terms of the 2-norm
    • \(d_{\mX}(x,x+r)\) is induced by the 2-norm, i.e. \(d_{\mX}(x,x+r)=\norm{x-(x+r)}_{2}\).
    • We may therefore ignore the denominator in the optimization problem
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

WGAN-ALP

  • Following miyato2019virtual one can for every \(x\) find an approximation \(\epsilon r_{k}\approx r'\), where \(\epsilon\sim p_{\epsilon}\) and \[r_{i+1}=\vt{\frac{\grad_{r}d_{\mY}(f(x),f(x+r))}{\norm{\grad_{r}d_{\mY}(f(x),f(x+r))}_{2}}}_{r=\xi r_{i}}\]
    • \(r_{0}\) is a random unit vector, and \(k=1\) is empirically found to be sufficient

  • Add ALP to encourage Lipschitz continuity for WGAN,

    \[ h(\theta,\phi)=\E_{p_\mr{true}}\br{f_{\phi}} - \E_{p_{\theta}}\br{f_\phi} + \lambda\E_{x\sim p_{\mr{r,g}}}\br{\mL_{\mr{ALP}}(\phi,x)},\] where \(p_{\mr{r,g}}\) is some combination of \(p_{\mr{true}}\) and \(p_{\theta}\) and \[\mL_{\mr{ALP}}(\phi,x)=\max\paren{0,\frac{d_{\mY}(f_{\phi}(x),f_{\phi}(x+r'))}{d_{\mX}(x,x+r')} - K},\]

    with \(d_{\mY}(f(x),f(x+r'))=\abs{f(x)-f(x+r')}\) and \(d_{\mX}(x,x+r')=\norm{x-(x+r')}_{2}=\norm{r'}_{2}\)

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Experiments

Experimental setup

  • Similar experimental setup as for WGAN-GP
  • Regularizer strength: \(\lambda=100\)
  • Lipschitz constant: \(K=1\)
  • For finding \(r'\): \(\xi=10\), \(p_{\epsilon}=\mU(0.1,10)\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

CIFAR-10

cifar10_images.png

Figure 1: Random samples using WGAN-ALP with (a) and without (b) batch normalization (BN).

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Comparison to other methods

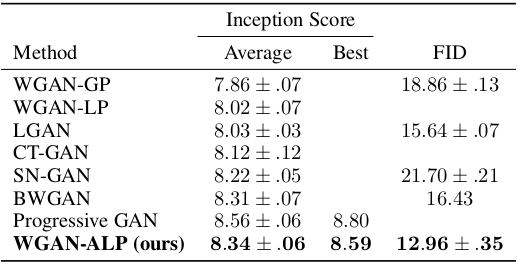
cifar10_table.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Remaining issues

  • Still have an expectation to enforce Lipschitz continuity \[\E_{x\sim p_{\mr{r,g}}}\br{L_{\mr{ALP}}(\phi,x)}=\E_{x\sim p_{\mr{r,g}}}\br{\max\paren{0,\frac{d_{\mY}(f_{\phi}(x),f_{\phi}(x+r'))}{d_{\mX}(x,x+r')} - K}}\]
    • How to do away with that as well?
  • The upper bound on \(r\) to ensure \(x+r\in\mX\), which the ability to find the maximum violation of the Lipschitz constraint
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

References

Andreas Munk, amunk@cs.ubc.ca, ammunk.com