Physics-guided Neural Networks (PGNN)

Anuj Karpatne*, William Watkins†, Jordan Read†, & Vipin Kumar*

*Department of Computer Science, University of Minnesota, †United States Geological Survey

Presented By

Andreas Munk

April 12, 2021

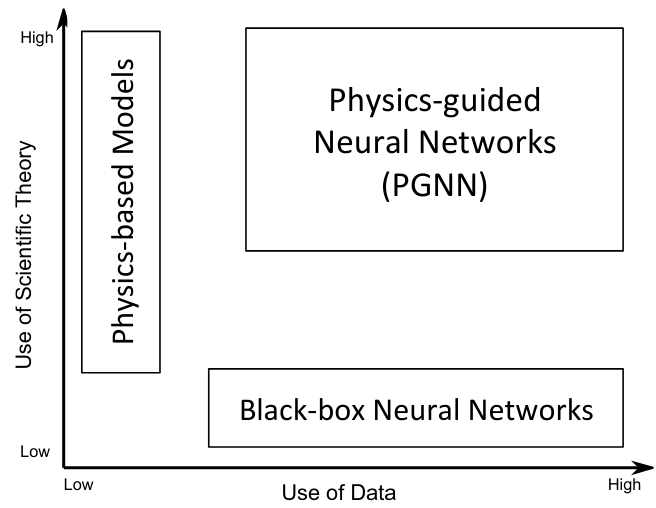
Where is the physics in modern machine learning?

  • Neural networks (NN) are used for black-box modeling to solve regression and classification problems
  • We cannot know if NNs even approximately captures underlying physical mechanics
    • Even if they produce small test scores (e.g. mean-square-error (MSE))
  • This obfuscates the functional relationship between input (\(x\)) and output (\(y\)) variables
    • Potentially impedes further scientific discoveries
    • Arguably, this “issue” is less relevant when modeling a statistical relationship between \(x\) and \(y\) - i.e. \(p_{\theta}(y|x)\).

      • Assume a “true” functional relationship between \(x\) and \(y\) with a noise term, \[y = f(x) + \epsilon\]

        Any discrepancy between a learned function \(f_{\theta}\) and the true function \(f\) may be summarized as uncertainty associated with \(p_{\theta}(y|x)\)

  • The perspective taken in this presentation is that we care about the functional relation between \(x\) and \(y\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Phisycs-guided Neural Networks (PGNN) karpatne2017physics

  • Combine neural networks with scientific knowledge of physics-based models
  • Introduce an additional loss term that penalizes “flawed” relationships between input and output variables under the neural network model
    • The penalization is defined using known physical mechanics underlying the problem at hand
    • These mechanics do not (necessarily) solve the problem, but encode certain relationship between (subsets) of the variables involved
  • This framework can effectively be viewed as constraining the training of the neural networks
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

pgnn_difference.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

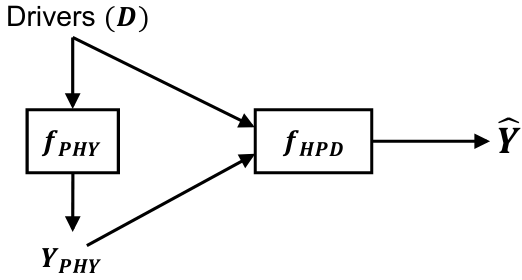
Constructing Hybrid-Physics-Data models

  • Consider input variables (observable data or “drivers”) \(D\in\gD\) and target variable(s) \(Y\in\gY\)
  • Standard neural network model
    • \(f_{\mr{NN}}:\gD \rightarrow \gY\) with parameters \(\theta_{\mr{NN}}\)
  • physics-based model
    • \(f_{\mr{PHY}}:\gD \rightarrow \gY\)
  • Hybrid model
    • \(f_{\mr{HPD}}:\gX=\gD\times\gY \rightarrow \gY\) with parameters \(\theta_{\mr{HPD}}\)
    • Also takes outputs from the physics based model
  • Define \(\hat{Y}_{\mr{NN}}=f_{\mr{NN}}(D)\) and \(\hat{Y}_{\mr{HPD}}=f_{\mr{HPD}}(D,\hat{Y}_{\mr{NN}})\)

pgnn_inputs.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Using physics-based loss functions

  • Consider the following minimization problem

    \[ \argmin_{\theta_{i}} \gL(\theta_{i})=\argmin_{\theta_{i}} \underbrace{\gL_{\mr{standard}}(\theta_{i})}_{\mr{"standard~loss"}} + \underbrace{\lambda R(\theta_{i})}_{\mr{regularization}} + \underbrace{\lambda_{\mr{PHY}}\gL_{\mr{PHY}}(\theta_{i})}_{\mr{Physical~Inconsistency}}, \quad i\in\tub{\mr{NN},\mr{HPD}}, \]

    with \(\lambda\) and \(\lambda_{\mr{PHY}}\) being hyperparameters

  • The Physical Inconsistency “measures constraint violations”
    • Define equality and inequality constraints \[ \gG(Y,D) = 0 \quad \gH(Y, D) \leq 0 \]
    • Both \(\gG\) and \(\gH\) are generic forms of physics-based (differentiable) equations. Both forms captures a physics-based relationship between the variable \(D\) and \(Y\).
      • For instance let \(D\) describe time and Y the position of an object. If we know that the object moves with constant velocity (\(v\)) we can describe it’s position according to \(Y=f(D)=v\cdot D + Y_{0}\).
      • Use the knowledge of the velocity to relate \(Y\) and \(D\), e.g. \(\gG(Y,D)=Y-(v\cdot D + Y_{0})\Rightarrow \gG(f(D),D)=0\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com
  • Leading to the following loss term (framed as soft constraints)

\[ \gL_{\mr{PHY}}(\theta_{i}) = \norm{\gG(f_{\mr{i}}(D),D)}^{2} + \mr{ReLU}(\gH(f_{\mr{i}}(D),D)) \quad i\in\tub{\mr{NN},\mr{HPD}} \]

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Experiments

Lake temperature modeling

  • Predict lake temperatures \(Y\) using PGNN

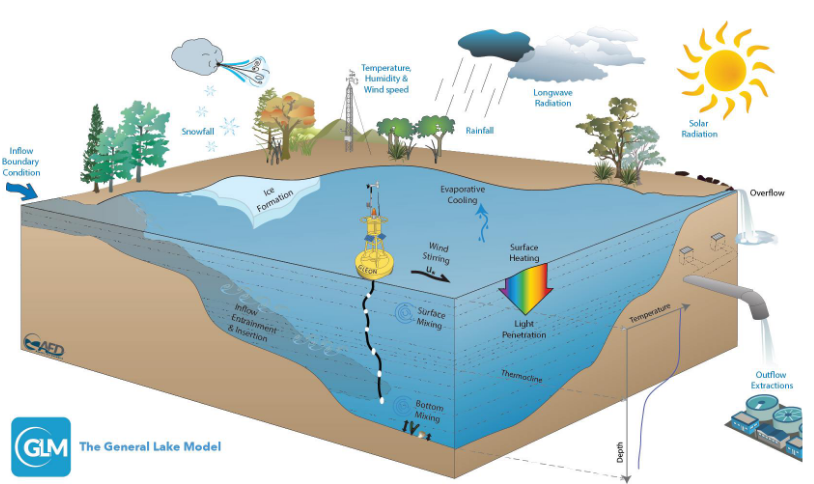
pgnn_watersystem.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

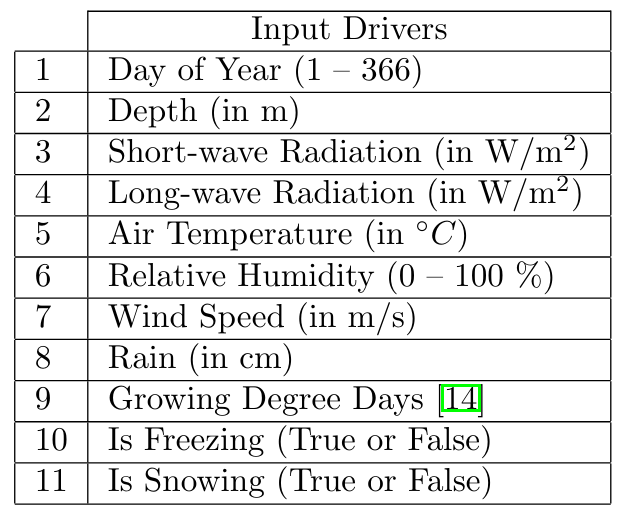
inputs.png

Figure 1: Input variables \(D\)

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Physical inconsistency for lake temperature modeling

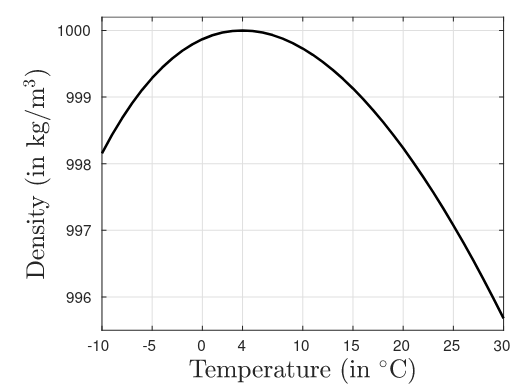
Temperature-density relationship of water

\begin{equation}\label{eq:rho} \rho(T) = 1000\times \paren{1-\frac{(T+288.9414)(T-3.9863)^{2}}{508929.2(T+68.12963)}} \end{equation}

pgnn_temp.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Denisty-depth relationship

  • Density is monotonically increasing with depth

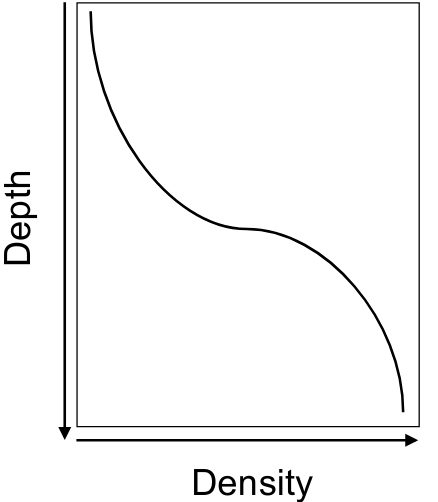
pgnn_density_depth.png

Figure 2: Sketch of depth and density relationship

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

  • Consider two depths \(d_{1}\) and \(d_{2}\) at time \(t\), then the density as a function of depth and time \(t\) must satisfy

    \[ \rho(d_{1},t) - \rho(d_{2},t) \leq 0, \quad d_{1} \leq d_{2} \]

  • We can use the above requirement to construct the inequality constraint \(\gH\)
    • Consider the regular grid of \(n_{d}\) depth values and \(n_{t}\) time-steps
    • Consider \(\hat{\rho}(d_{k},t)=\rho(f_{i}(D))\), where \(\rho(\cdot)\) is from \eqref{eq:rho}, the depth value and time value in \(D\) are equal \(d_{k}\) and \(t\) respectively, and \(f\) is a function, e.g. \(f_{\mr{PHY}}\)
    • Define \(\Delta(k, t) = \hat{\rho}(d_{k}, t) - \hat{\rho}(d_{k+1}, t)\), with \(k\in\tub{1,\dots,n_{d}}\)

  • The physics regularized loss term then becomes

    \[ \gL_{\mr{PHY}}(\theta_{i}) = \frac{1}{n_{t}(n_{d}-1)}\sum_{t=1}^{n_{t}}\sum_{k}^{n_{d}-1}\mr{ReLU}(\Delta(k,t)), \]

    • Which we can differentiate with respect to \(\theta_{i}\)
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Loss function for lake temperature modeling

\begin{align*} \gL_{\mr{stand}}(\theta_{i}) &= \frac{1}{n}\sum_{k=1}^{n}\paren{y_{i}-f_{i}(x_{i})}^{2}, \\ R(\theta_{i}) &= \lambda_{1}\norm{\theta_{i}}_{1} + \lambda_{2}\norm{\theta_{i}}_{2}, \\ \gL_{\mr{PHY}}(\theta_{i}) &= \frac{1}{n_{t}(n_{d}-1)}\sum_{t=1}^{n_{t}}\sum_{k}^{n_{d}-1}\mr{ReLU}(\Delta(k,t)), \end{align*}
  • \(n\) is number of data points
  • \(n_{d}\) is the number of unique depth measurements (different depth values)
  • \(n_{t}\) is the number of unique time measurements (day of year)
  • \(\Delta(k,t)\) is part of the physical inconsistency loss, as defined earlier
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Results

Models and their notation

  • NN, SVM, LSBoost: to a standard neural network model trained without physical knowledge, support vector machines, and least squared boosted regression tress
  • PHY: A state-of-the-art general lake model (simulator)
  • PGNN0: uses \(f_{\mr{PHY}}\) (i.e. takes simulated temperatures as additional arguments), but does not use \(\gL_{\mr{PHY}}\)
  • PGNN: The proposed method
  • Define the physical inconsistency metric - a number representing the fraction of times the density constraint is violated
Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Root mean squared error (RMSE) and physical inconsistency

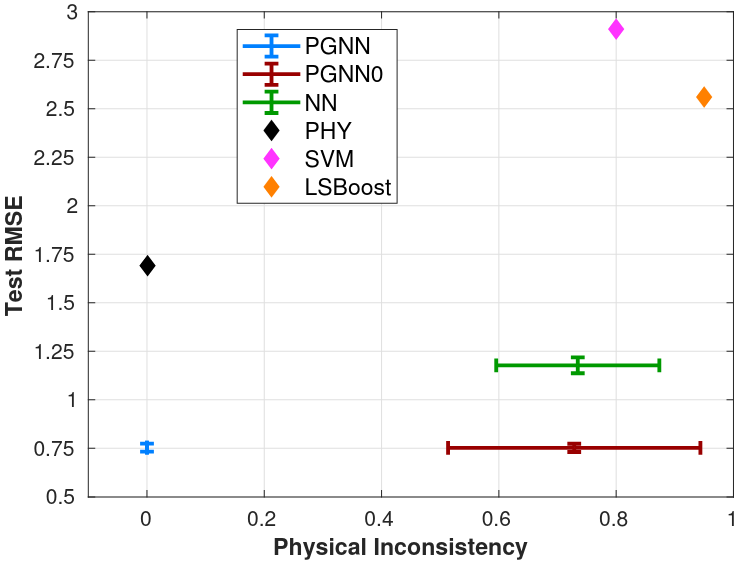
pgnn_lake_mille.png

Figure 3: Lake Mille Lacs

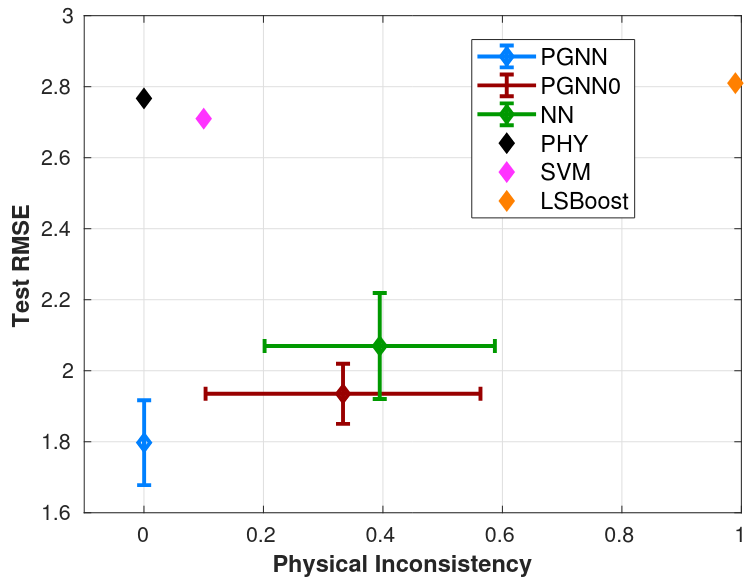
pgnn_lake_mendota.png

Figure 4: Lake Mendota

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Relation to training size (Lake Mille Lacs)

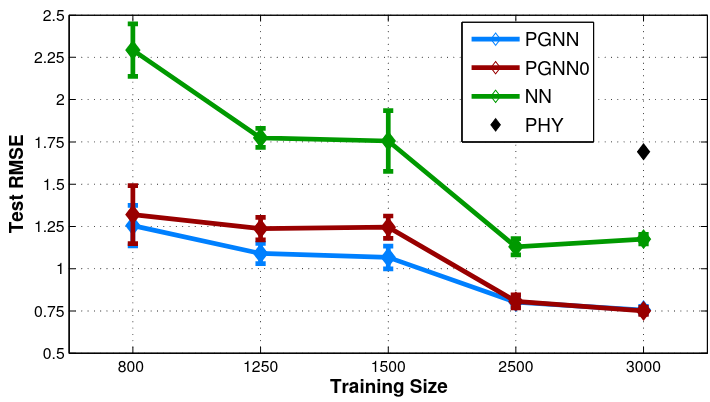
pgnn_size_mse.png

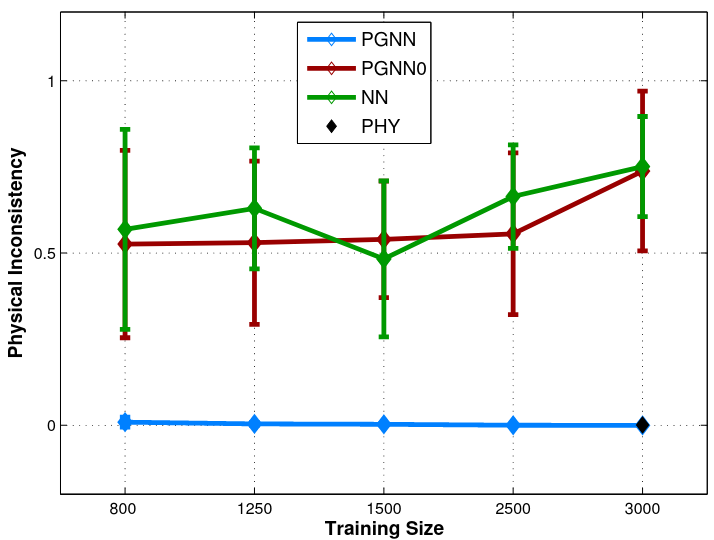
pgnn_consistency_size.png

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

Density-depth relationship

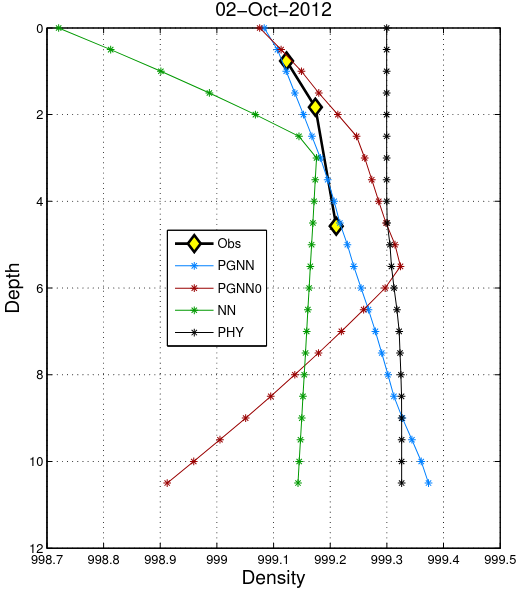
pgnn_depth_dens_profile_mille.png

Figure 5: Lake Mille Lacs

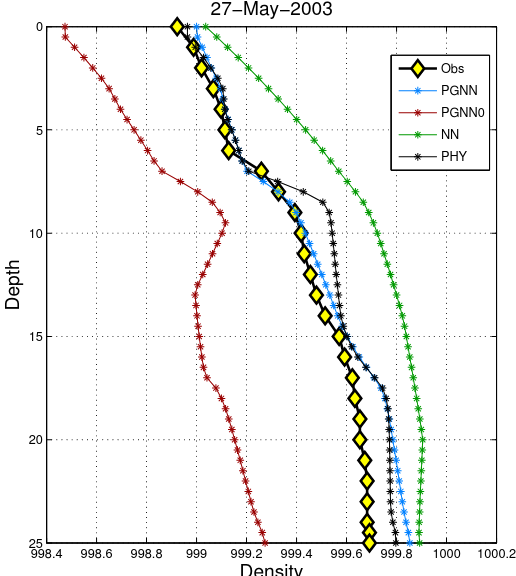
pgnn_depth_dens_mendota.png

Figure 6: Lake Mendota

Andreas Munk, amunk@cs.ubc.ca, ammunk.com

References

Andreas Munk, amunk@cs.ubc.ca, ammunk.com