Probabilistic Surrogate Networks for Simulators with Unbounded Randomness
Andreas Munk, Berend Zwartsenberg, Adam Ścibior, Atılım Güneş Baydin,
Andrew Stewart, Goran Fernlund,
Anoush Poursartip, Frank Wood
amunk@cs.ubc.ca
January 13, 2022
\( \newcommand{\ie}{i.e.} \newcommand{\eg}{e.g.} \newcommand{\etal}{\textit{et~al.}} \newcommand{\wrt}{w.r.t.} \newcommand{\bra}[1]{\langle #1 \mid} \newcommand{\ket}[1]{\mid #1\rangle} \newcommand{\braket}[2]{\langle #1 \mid #2 \rangle} \newcommand{\bigbra}[1]{\big\langle #1 \big\mid} \newcommand{\bigket}[1]{\big\mid #1 \big\rangle} \newcommand{\bigbraket}[2]{\big\langle #1 \big\mid #2 \big\rangle} \newcommand{\grad}{\boldsymbol{\nabla}} \newcommand{\divop}{\grad\scap} \newcommand{\pp}{\partial} \newcommand{\ppsqr}{\partial^2} \renewcommand{\vec}[1]{\boldsymbol{#1}} \newcommand{\trans}[1]{#1^\mr{T}} \newcommand{\dm}{\,\mathrm{d}} \newcommand{\complex}{\mathbb{C}} \newcommand{\real}{\mathbb{R}} \newcommand{\krondel}[1]{\delta_{#1}} \newcommand{\limit}[2]{\mathop{\longrightarrow}_{#1 \rightarrow #2}} \newcommand{\measure}{\mathbb{P}} \newcommand{\scap}{\!\cdot\!} \newcommand{\intd}[1]{\int\!\dm#1\: } \newcommand{\ave}[1]{\left\langle #1 \right\rangle} \newcommand{\br}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\paren}[1]{\left(#1\right)} \newcommand{\tub}[1]{\left\{#1\right\}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\evalat}[1]{\left.#1\right\vert} \newcommand*{\given}{\mid} \newcommand{\abs}[1]{\left\lvert#1\right\rvert} \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \newcommand{\figleft}{\em (Left)} \newcommand{\figcenter}{\em (Center)} \newcommand{\figright}{\em (Right)} \newcommand{\figtop}{\em (Top)} \newcommand{\figbottom}{\em (Bottom)} \newcommand{\captiona}{\em (a)} \newcommand{\captionb}{\em (b)} \newcommand{\captionc}{\em (c)} \newcommand{\captiond}{\em (d)} \newcommand{\newterm}[1]{\bf #1} \def\ceil#1{\lceil #1 \rceil} \def\floor#1{\lfloor #1 \rfloor} \def\1{\boldsymbol{1}} \newcommand{\train}{\mathcal{D}} \newcommand{\valid}{\mathcal{D_{\mathrm{valid}}}} \newcommand{\test}{\mathcal{D_{\mathrm{test}}}} \def\eps{\epsilon} \def\reta{\textnormal{$\eta$}} \def\ra{\textnormal{a}} \def\rb{\textnormal{b}} \def\rc{\textnormal{c}} \def\rd{\textnormal{d}} \def\re{\textnormal{e}} \def\rf{\textnormal{f}} \def\rg{\textnormal{g}} \def\rh{\textnormal{h}} \def\ri{\textnormal{i}} \def\rj{\textnormal{j}} \def\rk{\textnormal{k}} \def\rl{\textnormal{l}} \def\rn{\textnormal{n}} \def\ro{\textnormal{o}} \def\rp{\textnormal{p}} \def\rq{\textnormal{q}} \def\rr{\textnormal{r}} \def\rs{\textnormal{s}} \def\rt{\textnormal{t}} \def\ru{\textnormal{u}} \def\rv{\textnormal{v}} \def\rw{\textnormal{w}} \def\rx{\textnormal{x}} \def\ry{\textnormal{y}} \def\rz{\textnormal{z}} \def\rvepsilon{\mathbf{\epsilon}} \def\rvtheta{\mathbf{\theta}} \def\rva{\mathbf{a}} \def\rvb{\mathbf{b}} \def\rvc{\mathbf{c}} \def\rvd{\mathbf{d}} \def\rve{\mathbf{e}} \def\rvf{\mathbf{f}} \def\rvg{\mathbf{g}} \def\rvh{\mathbf{h}} \def\rvu{\mathbf{i}} \def\rvj{\mathbf{j}} \def\rvk{\mathbf{k}} \def\rvl{\mathbf{l}} \def\rvm{\mathbf{m}} \def\rvn{\mathbf{n}} \def\rvo{\mathbf{o}} \def\rvp{\mathbf{p}} \def\rvq{\mathbf{q}} \def\rvr{\mathbf{r}} \def\rvs{\mathbf{s}} \def\rvt{\mathbf{t}} \def\rvu{\mathbf{u}} \def\rvv{\mathbf{v}} \def\rvw{\mathbf{w}} \def\rvx{\mathbf{x}} \def\rvy{\mathbf{y}} \def\rvz{\mathbf{z}} \def\erva{\textnormal{a}} \def\ervb{\textnormal{b}} \def\ervc{\textnormal{c}} \def\ervd{\textnormal{d}} \def\erve{\textnormal{e}} \def\ervf{\textnormal{f}} \def\ervg{\textnormal{g}} \def\ervh{\textnormal{h}} \def\ervi{\textnormal{i}} \def\ervj{\textnormal{j}} \def\ervk{\textnormal{k}} \def\ervl{\textnormal{l}} \def\ervm{\textnormal{m}} \def\ervn{\textnormal{n}} \def\ervo{\textnormal{o}} \def\ervp{\textnormal{p}} \def\ervq{\textnormal{q}} \def\ervr{\textnormal{r}} \def\ervs{\textnormal{s}} \def\ervt{\textnormal{t}} \def\ervu{\textnormal{u}} \def\ervv{\textnormal{v}} \def\ervw{\textnormal{w}} \def\ervx{\textnormal{x}} \def\ervy{\textnormal{y}} \def\ervz{\textnormal{z}} \def\rmA{\mathbf{A}} \def\rmB{\mathbf{B}} \def\rmC{\mathbf{C}} \def\rmD{\mathbf{D}} \def\rmE{\mathbf{E}} \def\rmF{\mathbf{F}} \def\rmG{\mathbf{G}} \def\rmH{\mathbf{H}} \def\rmI{\mathbf{I}} \def\rmJ{\mathbf{J}} \def\rmK{\mathbf{K}} \def\rmL{\mathbf{L}} \def\rmM{\mathbf{M}} \def\rmN{\mathbf{N}} \def\rmO{\mathbf{O}} \def\rmP{\mathbf{P}} \def\rmQ{\mathbf{Q}} \def\rmR{\mathbf{R}} \def\rmS{\mathbf{S}} \def\rmT{\mathbf{T}} \def\rmU{\mathbf{U}} \def\rmV{\mathbf{V}} \def\rmW{\mathbf{W}} \def\rmX{\mathbf{X}} \def\rmY{\mathbf{Y}} \def\rmZ{\mathbf{Z}} \def\ermA{\textnormal{A}} \def\ermB{\textnormal{B}} \def\ermC{\textnormal{C}} \def\ermD{\textnormal{D}} \def\ermE{\textnormal{E}} \def\ermF{\textnormal{F}} \def\ermG{\textnormal{G}} \def\ermH{\textnormal{H}} \def\ermI{\textnormal{I}} \def\ermJ{\textnormal{J}} \def\ermK{\textnormal{K}} \def\ermL{\textnormal{L}} \def\ermM{\textnormal{M}} \def\ermN{\textnormal{N}} \def\ermO{\textnormal{O}} \def\ermP{\textnormal{P}} \def\ermQ{\textnormal{Q}} \def\ermR{\textnormal{R}} \def\ermS{\textnormal{S}} \def\ermT{\textnormal{T}} \def\ermU{\textnormal{U}} \def\ermV{\textnormal{V}} \def\ermW{\textnormal{W}} \def\ermX{\textnormal{X}} \def\ermY{\textnormal{Y}} \def\ermZ{\textnormal{Z}} \def\vzero{\boldsymbol{0}} \def\vone{\boldsymbol{1}} \def\vmu{\boldsymbol{\mu}} \def\vtheta{\boldsymbol{\theta}} \def\va{\boldsymbol{a}} \def\vb{\boldsymbol{b}} \def\vc{\boldsymbol{c}} \def\vd{\boldsymbol{d}} \def\ve{\boldsymbol{e}} \def\vf{\boldsymbol{f}} \def\vg{\boldsymbol{g}} \def\vh{\boldsymbol{h}} \def\vi{\boldsymbol{i}} \def\vj{\boldsymbol{j}} \def\vk{\boldsymbol{k}} \def\vl{\boldsymbol{l}} \def\vm{\boldsymbol{m}} \def\vn{\boldsymbol{n}} \def\vo{\boldsymbol{o}} \def\vp{\boldsymbol{p}} \def\vq{\boldsymbol{q}} \def\vr{\boldsymbol{r}} \def\vs{\boldsymbol{s}} \def\vt{\boldsymbol{t}} \def\vu{\boldsymbol{u}} \def\vv{\boldsymbol{v}} \def\vw{\boldsymbol{w}} \def\vx{\boldsymbol{x}} \def\vy{\boldsymbol{y}} \def\vz{\boldsymbol{z}} \def\evalpha{\alpha} \def\evbeta{\beta} \def\evepsilon{\epsilon} \def\evlambda{\lambda} \def\evomega{\omega} \def\evmu{\mu} \def\evpsi{\psi} \def\evsigma{\sigma} \def\evtheta{\theta} \def\eva{a} \def\evb{b} \def\evc{c} \def\evd{d} \def\eve{e} \def\evf{f} \def\evg{g} \def\evh{h} \def\evi{i} \def\evj{j} \def\evk{k} \def\evl{l} \def\evm{m} \def\evn{n} \def\evo{o} \def\evp{p} \def\evq{q} \def\evr{r} \def\evs{s} \def\evt{t} \def\evu{u} \def\evv{v} \def\evw{w} \def\evx{x} \def\evy{y} \def\evz{z} \def\mA{\boldsymbol{A}} \def\mB{\boldsymbol{B}} \def\mC{\boldsymbol{C}} \def\mD{\boldsymbol{D}} \def\mE{\boldsymbol{E}} \def\mF{\boldsymbol{F}} \def\mG{\boldsymbol{G}} \def\mH{\boldsymbol{H}} \def\mI{\boldsymbol{I}} \def\mJ{\boldsymbol{J}} \def\mK{\boldsymbol{K}} \def\mL{\boldsymbol{L}} \def\mM{\boldsymbol{M}} \def\mN{\boldsymbol{N}} \def\mO{\boldsymbol{O}} \def\mP{\boldsymbol{P}} \def\mQ{\boldsymbol{Q}} \def\mR{\boldsymbol{R}} \def\mS{\boldsymbol{S}} \def\mT{\boldsymbol{T}} \def\mU{\boldsymbol{U}} \def\mV{\boldsymbol{V}} \def\mW{\boldsymbol{W}} \def\mX{\boldsymbol{X}} \def\mY{\boldsymbol{Y}} \def\mZ{\boldsymbol{Z}} \def\mBeta{\boldsymbol{\beta}} \def\mPhi{\boldsymbol{\Phi}} \def\mLambda{\boldsymbol{\Lambda}} \def\mSigma{\boldsymbol{\Sigma}} \def\gA{\mathcal{A}} \def\gB{\mathcal{B}} \def\gC{\mathcal{C}} \def\gD{\mathcal{D}} \def\gE{\mathcal{E}} \def\gF{\mathcal{F}} \def\gG{\mathcal{G}} \def\gH{\mathcal{H}} \def\gI{\mathcal{I}} \def\gJ{\mathcal{J}} \def\gK{\mathcal{K}} \def\gL{\mathcal{L}} \def\gM{\mathcal{M}} \def\gN{\mathcal{N}} \def\gO{\mathcal{O}} \def\gP{\mathcal{P}} \def\gQ{\mathcal{Q}} \def\gR{\mathcal{R}} \def\gS{\mathcal{S}} \def\gT{\mathcal{T}} \def\gU{\mathcal{U}} \def\gV{\mathcal{V}} \def\gW{\mathcal{W}} \def\gX{\mathcal{X}} \def\gY{\mathcal{Y}} \def\gZ{\mathcal{Z}} \def\sA{\mathbb{A}} \def\sB{\mathbb{B}} \def\sC{\mathbb{C}} \def\sD{\mathbb{D}} \def\sF{\mathbb{F}} \def\sG{\mathbb{G}} \def\sH{\mathbb{H}} \def\sI{\mathbb{I}} \def\sJ{\mathbb{J}} \def\sK{\mathbb{K}} \def\sL{\mathbb{L}} \def\sM{\mathbb{M}} \def\sN{\mathbb{N}} \def\sO{\mathbb{O}} \def\sP{\mathbb{P}} \def\sQ{\mathbb{Q}} \def\sR{\mathbb{R}} \def\sS{\mathbb{S}} \def\sT{\mathbb{T}} \def\sU{\mathbb{U}} \def\sV{\mathbb{V}} \def\sW{\mathbb{W}} \def\sX{\mathbb{X}} \def\sY{\mathbb{Y}} \def\sZ{\mathbb{Z}} \def\emLambda{\Lambda} \def\emA{A} \def\emB{B} \def\emC{C} \def\emD{D} \def\emE{E} \def\emF{F} \def\emG{G} \def\emH{H} \def\emI{I} \def\emJ{J} \def\emK{K} \def\emL{L} \def\emM{M} \def\emN{N} \def\emO{O} \def\emP{P} \def\emQ{Q} \def\emR{R} \def\emS{S} \def\emT{T} \def\emU{U} \def\emV{V} \def\emW{W} \def\emX{X} \def\emY{Y} \def\emZ{Z} \def\emSigma{\Sigma} \newcommand{\etens}[1]{\mathsfit{#1}} \def\etLambda{\etens{\Lambda}} \def\etA{\etens{A}} \def\etB{\etens{B}} \def\etC{\etens{C}} \def\etD{\etens{D}} \def\etE{\etens{E}} \def\etF{\etens{F}} \def\etG{\etens{G}} \def\etH{\etens{H}} \def\etI{\etens{I}} \def\etJ{\etens{J}} \def\etK{\etens{K}} \def\etL{\etens{L}} \def\etM{\etens{M}} \def\etN{\etens{N}} \def\etO{\etens{O}} \def\etP{\etens{P}} \def\etQ{\etens{Q}} \def\etR{\etens{R}} \def\etS{\etens{S}} \def\etT{\etens{T}} \def\etU{\etens{U}} \def\etV{\etens{V}} \def\etW{\etens{W}} \def\etX{\etens{X}} \def\etY{\etens{Y}} \def\etZ{\etens{Z}} \newcommand{\pdata}{p_{\rm{data}}} \newcommand{\ptrain}{\hat{p}_{\rm{data}}} \newcommand{\Ptrain}{\hat{P}_{\rm{data}}} \newcommand{\pmodel}{p_{\rm{model}}} \newcommand{\Pmodel}{P_{\rm{model}}} \newcommand{\ptildemodel}{\tilde{p}_{\rm{model}}} \newcommand{\pencode}{p_{\rm{encoder}}} \newcommand{\pdecode}{p_{\rm{decoder}}} \newcommand{\precons}{p_{\rm{reconstruct}}} \newcommand{\laplace}{\mathrm{Laplace}} % Laplace distribution \newcommand{\E}{\mathbb{E}} \newcommand{\Ls}{\mathcal{L}} \newcommand{\R}{\mathbb{R}} \newcommand{\emp}{\tilde{p}} \newcommand{\lr}{\alpha} \newcommand{\reg}{\lambda} \newcommand{\rect}{\mathrm{rectifier}} \newcommand{\softmax}{\mathrm{softmax}} \newcommand{\sigmoid}{\sigma} \newcommand{\softplus}{\zeta} \newcommand{\KL}{D_{\mathrm{KL}}} \newcommand{\Var}{\mathrm{Var}} \newcommand{\standarderror}{\mathrm{SE}} \newcommand{\Cov}{\mathrm{Cov}} \newcommand{\normlzero}{L^0} \newcommand{\normlone}{L^1} \newcommand{\normltwo}{L^2} \newcommand{\normlp}{L^p} \newcommand{\normmax}{L^\infty} \newcommand{\parents}{Pa} % See usage in notation.tex. Chosen to match Daphne's book. \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\Tr}{Tr} \let\ab\allowbreak \newcommand{\vxlat}{\vx_{\mr{lat}}} \newcommand{\vxobs}{\vx_{\mr{obs}}} \newcommand{\block}[1]{\underbrace{\begin{matrix}1 & \cdots & 1\end{matrix}}_{#1}} \newcommand{\blockt}[1]{\begin{rcases} \begin{matrix} ~\\ ~\\ ~ \end{matrix} \end{rcases}{#1}} \newcommand{\tikzmark}[1]{\tikz[overlay,remember picture] \node (#1) {};} \)
Types of Simulators

Probabilistic programs and automatic inference - an example le2016inference

PyProb - https://github.com/pyprob/pyprob/tree/master/pyprob

Addresses Uniquely Identifies Random Variables van2018introduction

- Infer the posterior distribution \(p(\vx_{\mr{lat}}|\vx_{\mr{obs}})\) over latent variables \(\vx_{\mr{lat}}\) (specified by sample statements) conditioned on observed variables \(\vx_{\mr{obs}}\) (specified by observe statements)
- We consider the joint distribution over the space of “traces” \((x_{a_t}, a_t)\) for \(t=1,\dots,T\) \[p(\vx, \va) = \prod_{t=1}^T p(a_t|x_{a_1:a_{t-1}},a_{1:t-1}) p(x_{a_t}|x_{a_1:a_{t-1}},a_{1:t})\]
- We denoted the set of all variables \(\vx=\vx_{\mr{lat}}\cup\vx_{\mr{obs}}\)
- Address transitions are deterministic: \(p(a_t|x_{a_1:a_{t-1}},a_{1:t-1})\) is a Kronecker-Delta function
- But this notation becomes useful later
Sequential Importance Sampling
- Draw \(K\) samples \(\vx_{\mr{lat}}^k \overset{i.i.d.}{\sim}q(\vx_{\mr{lat}}|\vx_{\mr{obs}})\) (proposal distribution)
- Compute the weights, \[w^k = \frac{p(\vx_{\mr{lat}}^k,\vx_{\mr{obs}})}{q(\vx_{\mr{lat}}^k|\vx_{\mr{obs}})}\]
- Approximate the posterior as \[ p(\vx_{\mr{lat}}|\vx_{\mr{obs}})\approx\frac{\sum_{k=1}^Kw^k\delta(\vx_{\mr{lat}}^k-\vx_{\mr{lat}})}{\sum_{k=1}^Kw^k}\]
Sequential Importance Sampling and Evaluation Based Inference
- SIS in evaluation based inference engines involves calculating the weights as \[ w^k=\frac{p(\vx,\va)}{q(\vx_{\mr{lat}}^k,\va|\vx_{\mr{obs}})}=\frac{\prod_{t=1}^T p(a_t|x_{\lt a_{t}},a_{\lt t})p(x_{a_t}|x_{\lt a_{t}},a_{\lt t})} {\prod_{x_{a_t}^{\mr{lat}}\in\vx_{\mr{lat}}}q(x^{\mr{lat}}_{a_t}|x^{\mr{lat}}_{\lt a_t},a_{\lt t},\vx_{\mr{obs}})\prod_{t=1}^{T}q(a_{t}|x_{\lt a_{t}},a_{\lt t})}\]
- Where \(q(a_{t}|x_{\lt a_{t}},a_{\lt t})=p(a_{t}|x_{\lt a_{t}},a_{\lt t})\),
- Proposing from \(q\) requires executing the program
- \(K\) samples requires \(K\) evaluations of the program
Inference Compilation (IC) le2016inference
- IC is all about constructing \(q(\vx_{\mr{lat}}, \va|\vx_{\mr{obs}})\) \(\rightarrow\) efficient SIS \[q(\vx_{\mr{lat}},\va|\vx_{\mr{obs}};\phi) = q(\vx_{\mr{lat}},\va|\vx_{\mr{obs}};\phi) = \prod_{x_{a_t}^{\mr{lat}}\in\vx_{\mr{lat}}}q(x^{\mr{lat}}_{a_t}|\eta_{a_t}(x^{\mr{lat}}_{\lt a_t},a_{\lt t},\vx_{\mr{obs}};\phi))\prod_{t=1}^{T}q(a_{t}|x_{\lt a_{t}},a_{\lt t})\]
- \(\eta_{a_{t}}(\cdot)\) is a recurrent neural network
- We train \(q(\cdot|\vx_{\mr{obs}};\phi)\) to be close to \(p(\cdot|\vx_{\mr{obs}})\) for all
\(\vx_{\mr{obs}}\),
by minimizing the expected KL divergence under the marginal \(p(\vx_{\mr{obs}})\) \[\begin{align}\mL_{\mr{IC}}(\phi)&=\E_{p(\vx_{\mr{obs}})}\br{\mr{KL}\paren{p(\vx_{\mr{lat}},\va|\vx_{\mr{obs}})||q(\vx_{\mr{lat}},\va|\vx_{\mr{obs}};\phi)}}\nonumber\\ &=-\E_{p(\vx,\va)}\br{\log q(\vx_{\mr{lat}},\va|\vx_{\mr{obs}};\phi)} + \mr{const}\nonumber\end{align}\]
Probabilistic Surrogate Network (PSN)
- Evaluation-based inference (IC) is still limited by the execution speed of the program
- How about learning a surrogate model \(s\) that replaces \(p\) as a program when \(p\) is slow?
- We structure \(s\) as a distribution over traces factorized exactly like \(p\) \[ s(\vx,\va;\theta)=\prod_{t=1}^{T}s(x_{a_t}|\xi_{a_t}(x_{\lt a_{t}},a_{\leq t};\theta))s(a_t|\zeta_{a_t}(x_{\lt a_{t}},a_{\lt t};\theta))\]
- \(\xi_{a_t}(\cdot)\) and \(\zeta_{a_{t}}(\cdot)\) are recurrent neural networks
- Now we have to model the address transitions \(s(a_t|\zeta_{a_t}(x_{\lt a_{t}},a_{\lt t};\theta))\)
- For instance a categorical distribution
- We match \(p\) and \(s\) by minimizing the KL-divergence \[\begin{align*} \mL(\theta) &= \mr{KL}\paren{p(\vx,\va)||s(\vx,\va;\theta)} \\ &= -\E_{p(\vx,\va)}\br{\log s(\vx,\va;\theta)} + \mr{const} \end{align*}\]
- Fully compatible with the probabilistic programming framework
The Communication Interface

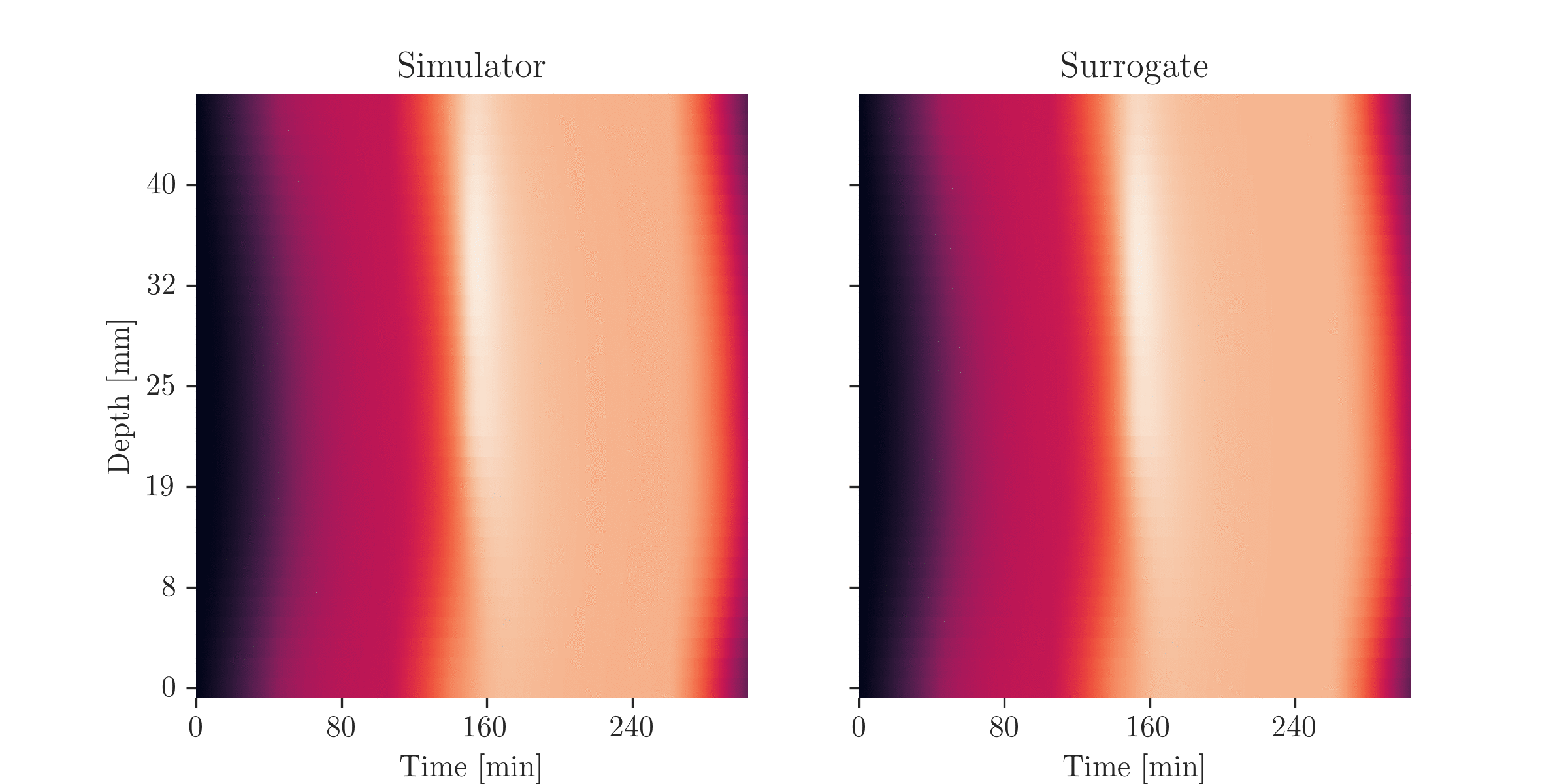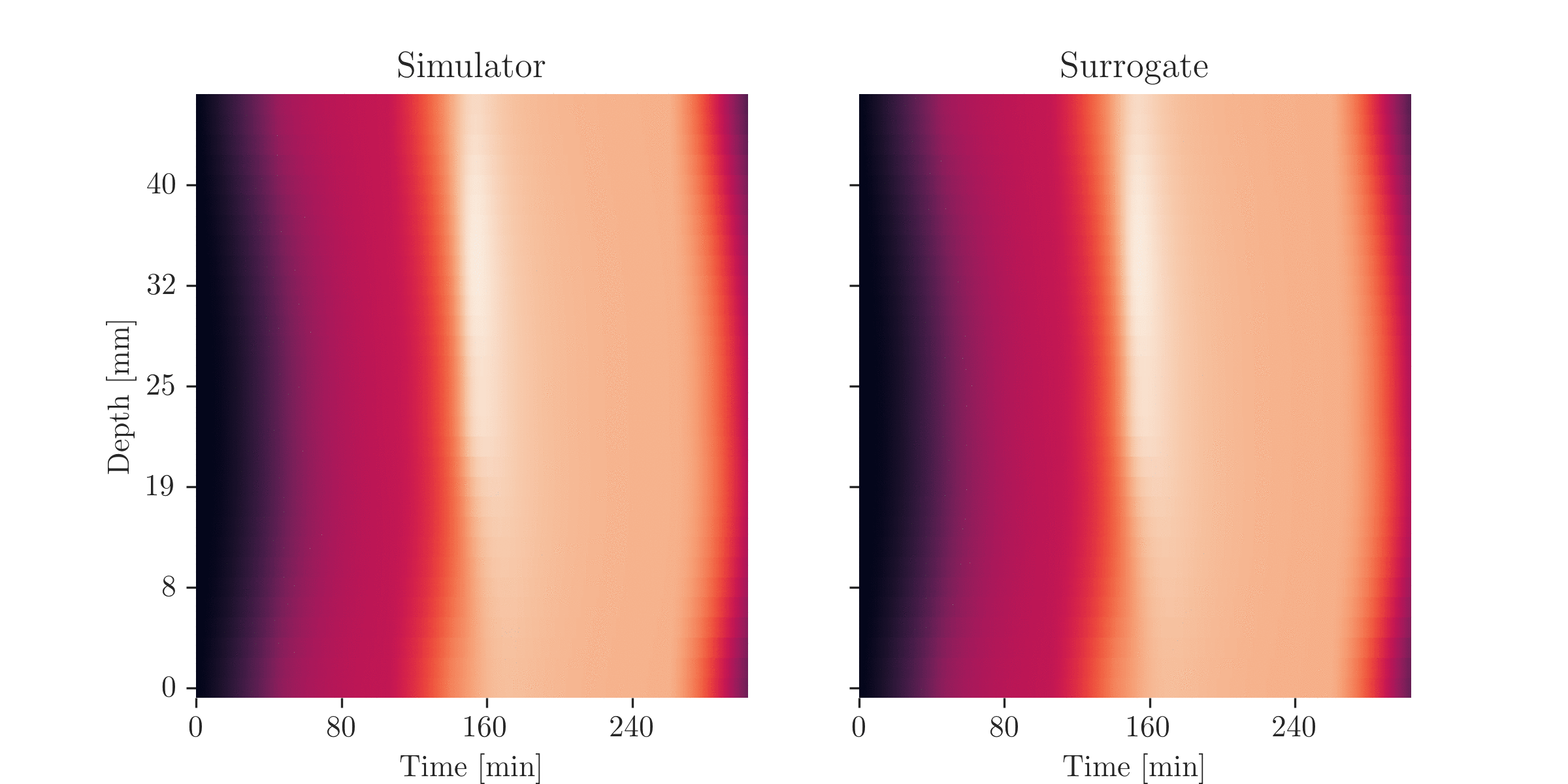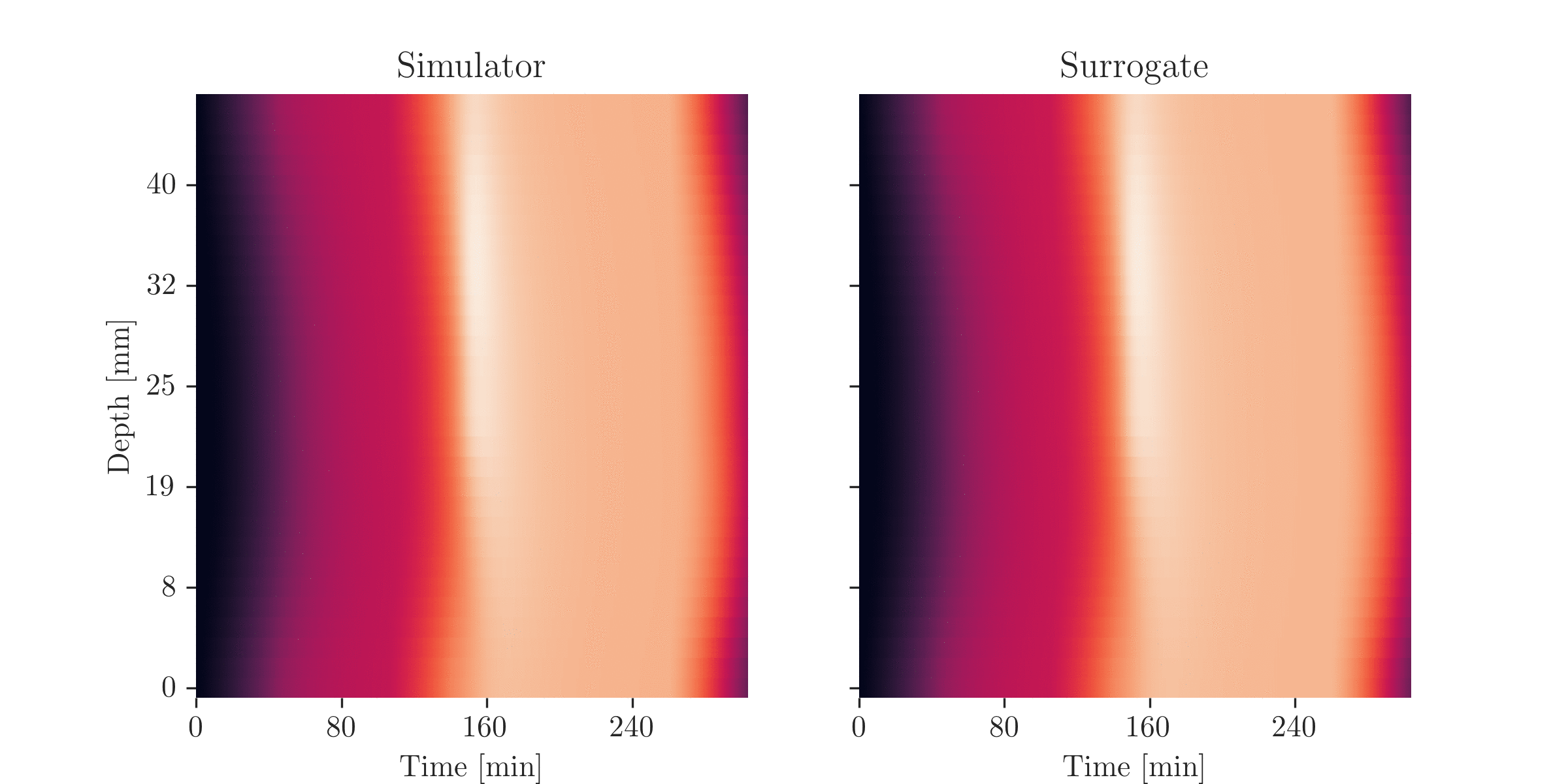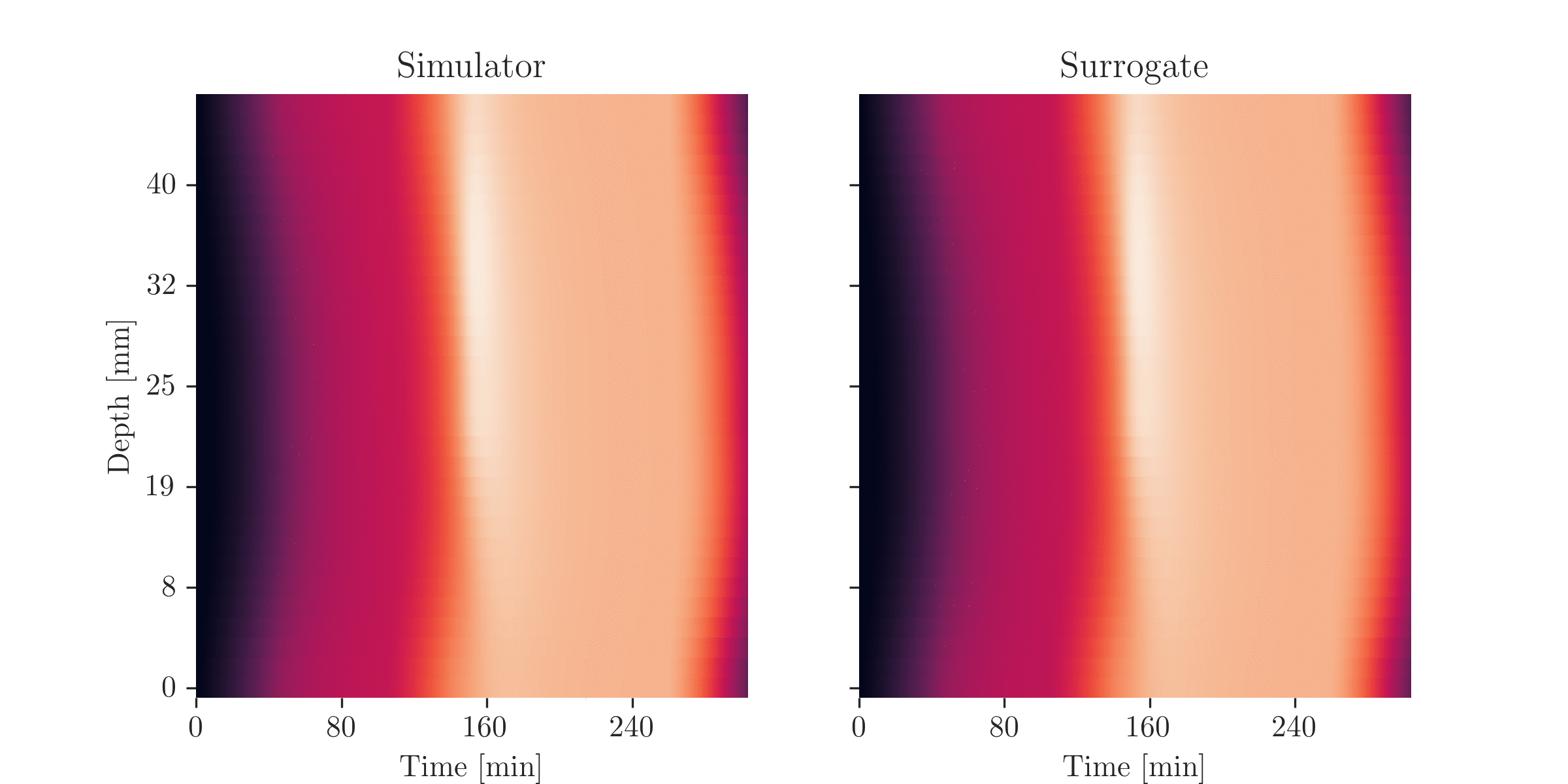
Simulating the Curing of Composite Materials

Faster Simulation
- ~90 times faster simulation
Faster Inference
- ~15 times faster inference
- Infer \(\E_{p(\vx_{\mr{lat}}|\vx_{\mr{obs}})}\br{\mu_w}\)
- \(\mu_w\) is the empirical mean of the temperature across the time window $w=\br{155,165}$min at a fixed depth $30$mm

Program Synthesis and Address Transitions

Control Flow Program

Address Transitions

Figure 1: Address transition graph generated by the original program

Figure 2: Address transition graph generated by the PSN